Most fish are ectothermic, or "cold blooded". Their body temperature matches the temperature around them. Certain species of sharks, however, have endothermic ("warm blooded") capabilites. Dr. Aaron Carlisle at the University of Delaware is performing research on these sharks, trying to gain a deeper understanding of their heat generating capabilities. The 3 species of shark that Dr. Carlisle is studying are the:

• White Shark (or Great White Shark)
• Salmon Shark
• Shortfin Mako Shark (hereafter simply the "Mako Shark")

These 3 species are able to use a specially developed network of blood vessels to retain the heat produced by their muscles, and can therefore maintain an internal body temperature warmer than that of the surrounding water. Analyzing the heat generating capabilities of these species may lead to more accurate predictions of what waters these sharks are able to navigate, especially as the ocean temperatures change with climate conditions.

Dr. Carlisle's original analysis assumed that the generation taking place throughout the shark's body was evenly distributed. It was brought to his attention, however, that in actuality, this is not the case. The heat generation occurs in concentrated pockets of red muscle, and then the warmed blood is distributed throughout the shark's body.

To see how much of a difference this would make to the end result, I set up a heat transfer analysis script in python, using a finite difference method to numerically approximate the differential equations involved in conduction heat transfer. The script could be used to compare concentrated and distributed heat generation in each of the 3 selected species of shark under varying ambient temperatures. While certainly less detailed than a full simulation, this sort of estimation should clearly show if uniform and concentrated heat generation cases produce similar results. Since we're dealing with conduction, the equation in question is Fourier's Law:

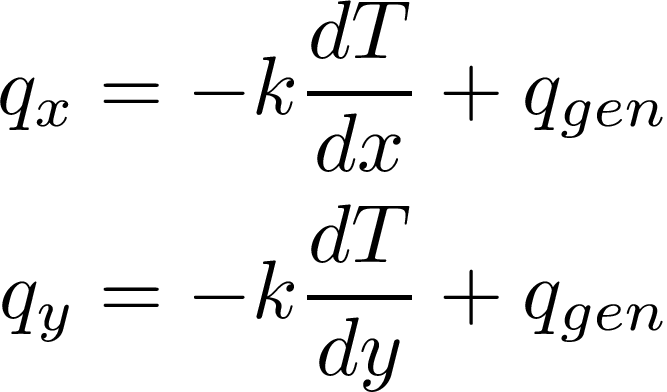
To perform the finite difference method, and to make the programming easier, we assumed a square cross-sectional profile of a shark. The size varied by species. This square was then turned into a grid of smaller squares. Each of these small squares, or "elements," was one node in our finite difference calculation. Each node was one of three types: internal, edge, or corner.

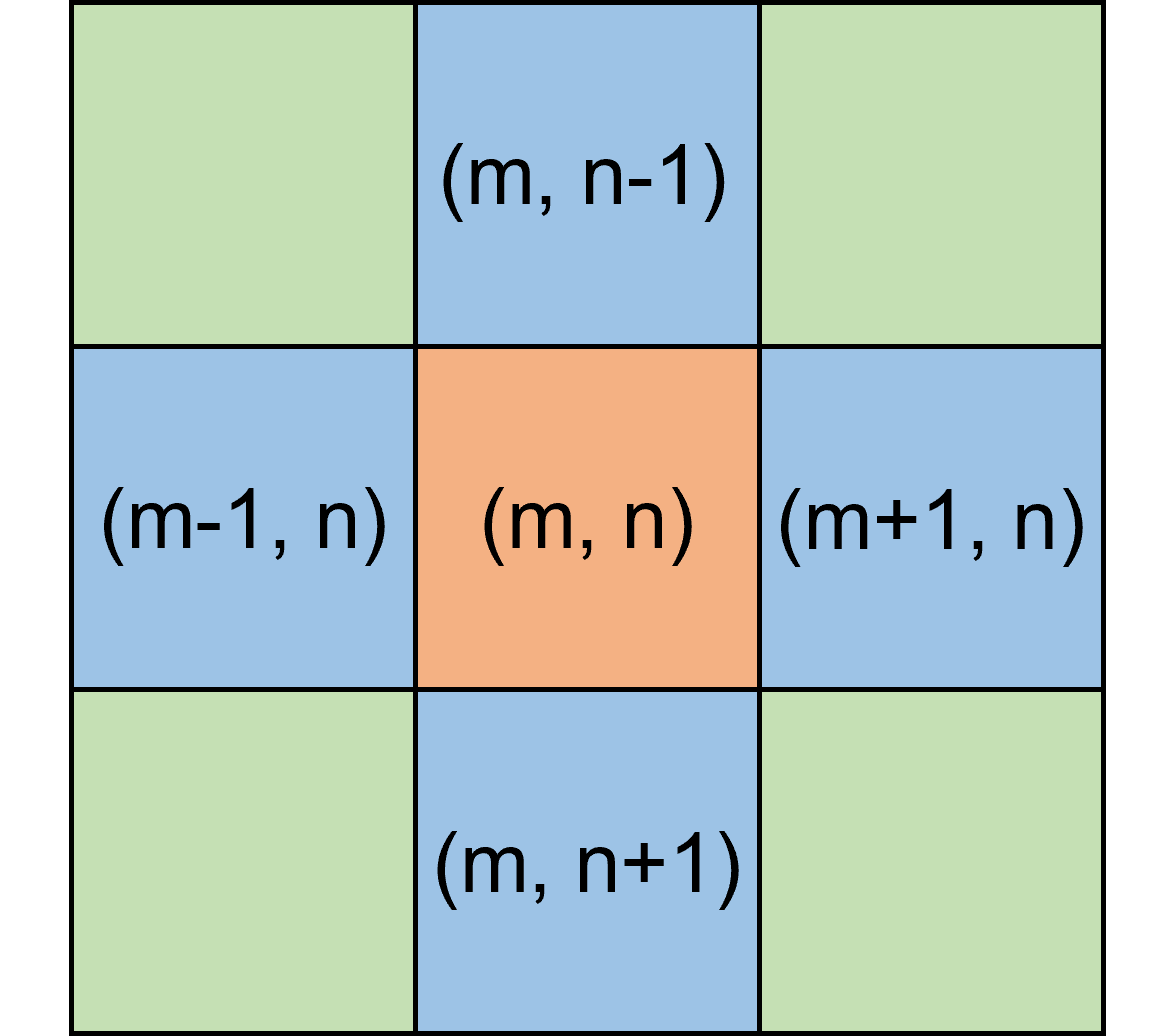
The finite difference method is an iterative, fixed-point solver. Each iteration, the finite element grid is updated. For each node, the new temperature is found by applying the conductive heat transfer equation to each of its four edges. Special consideration is given to the edge and corner nodes, as some of their edges interface with the environment (here assumed to be ocean water at a constant temperature), instead of recieving heat from or transfering heat to neighboring elements. The loop will run until the shark's temperature profile reaches steady state - this means that the change in temperature between iterations is negligible, or below a given threshold.

The primary purpose of these simulations was to output contour plots of the final steady-state profile, comparing uniform and distributed heat generation cases. Relevant parameters, such as ambient temperature, coefficient of heat transfer, etc. can be edited, but are kept constant between comparisons of generation type.

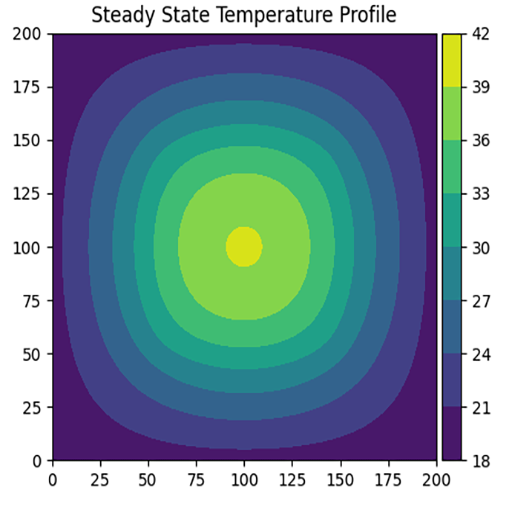
For the uniform case, each node in the grid has an equal heat generation term to all other nodes. For the concentrated case, the heat generation only occurs in a square in the center of the profile, approximately half the size of the whole square. Across both uniform and concentrated heat generation cases, the total amount of heat generation remains the same. Below, you can see an example uniform vs. concentrated generation comparison for a salmon shark.

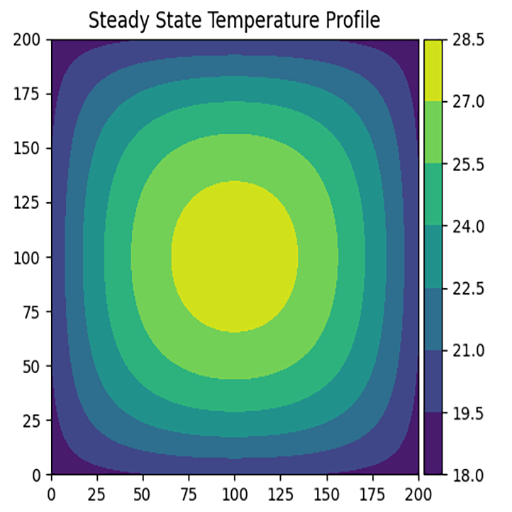
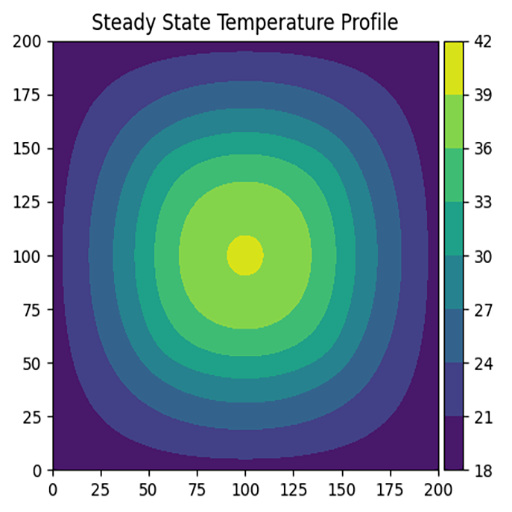
While the general contours appear similar, it is clear that in the concentrated generation case, the core temperature is much higher than in the uniform generation case. It is important to note that this simulation was run with placeholder values, however. We now know the finite difference solver works, and is capable of showing differences in steady state temperature - but before any conclusions can be made regarding Dr. Carlisle's research, the correct thermal properties of the shark must be sourced and plugged in.

Check out the whole project on GitHub!